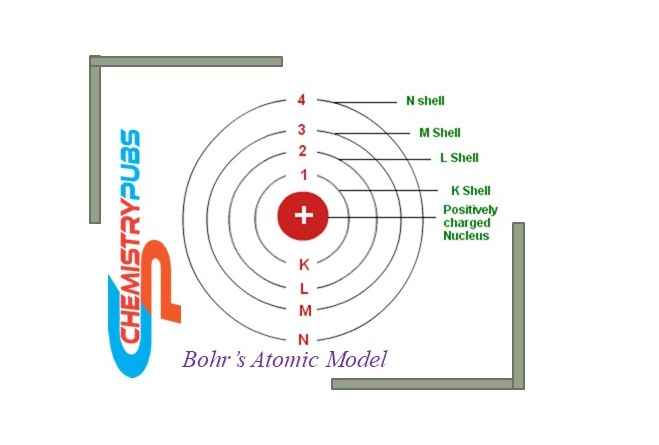
Bohrs atomic model relates the fixed atomic size and revolving negatively charged electrons in orbits around the nucleus. This model was given by Niels Bohr in 1913 to provide information on how electrons can revolve in a stable orbit around the nucleus of an atom.
Niels Bohr removed the limitations of Rutherford’s atomic model and proposed this model. The postulate of this model has the closest connection with Rutherford’s atomic model. So, this model is also called the Rutherford-Bohr Model.
The Bohrs atomic model is completely dependent on quantum mechanics. This model is the most important model to explain the atomic structure, though it contains some limitations.
This model can explain the formula of Rydberg for giving a clear idea about the spectral emission lines of atomic hydrogen.
What is the Bohrs atomic model?
The Bohrs atomic model is a developed model in which a positively charged nucleus stays in the center of the atom; whereas the negatively charged electrons revolve around the nucleus with fixed energy.
This model explains the properties of electrons in the atoms based on the certain allowed possible values. The absorption and emission of energy by the electron during the jumping between the energy levels can be understood by this model.
This modern developed model was proposed by Neil Bohr in 1913 who was a Danish physicist. He suggested that the electrons revolve in a predictable path called orbital shells in orbits. He gave the idea about electrons and the different energy levels associated with them.
According to this model, the positively charged nucleus is surrounded by the negatively charged particle electrons in fixed orbits. The electrons located near the positively charged nucleus contain less energy; whereas the electrons located far away from the nucleus contain more energy.
In 1922, Niels Bohr was awarded the Nobel Prize in Physics for inventing this atomic structure.
Diagram of The Bohrs Atomic Model

Postulates of the Bohrs Atomic Model
The main postulates of this atomic model are given below:
The negatively charged electrons revolve around the positively charged nucleus in stable orbits or shells without the emission of radiant energy. Each orbit contains a certain amount of energy which is called an energy shell or energy level.
The circular paths of electrons around the nucleus contain fixed levels of energy called orbital shells.
The energy shell or orbits are shown by n= 1, 2, 3, 4, …. (integers) and are known as quantum numbers. These quantum numbers are represented by K, L, M, and N for 1, 2, 3, and 4 respectively. The lowest energy level contains an n=1 quantum number which is called the ground energy state.
Therefore,
1st orbit (1st energy level) is generally represented as a K shell containing up to 2 electrons.
2nd orbit (2nd energy level) is generally represented as an L shell containing up to 8 electrons.
3rd orbit (3rd energy level) is generally represented as an M shell containing up to 18 electrons.
4th orbit (4th energy level) is generally represented as N Shell and contains up to 32 electrons.
The electrons in the ground energy level can jump to the higher energy level after gaining energy. But electrons can come out of the lower energy level after losing the energy.
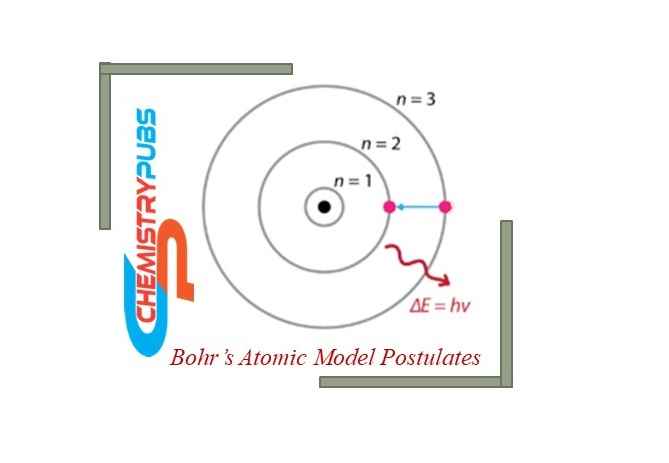
The absorption or emission of energy by the electrons around the nucleus is completely equal to the difference between the energies of the two energy levels (E1, E2) which can be determined by the following Plank’s equation.
ΔE = E2-E1 = h𝜈
Where,
ΔE = absorption or emission of energy by the electrons
h= Plank’s constant for this equation
𝜈= The electromagnetic frequency during the absorption or emission of energy by the electrons.
The angular momentum of every electron which revolves around the nucleus in energy shells is given by:
mevr = nh/2π
Where,
n= energy shell numbers and is represented by 1, 2, 3, 4, …..
me= The electronic mass
v= The velocity of the electron
r= The radius of the energy shell
h= Plank’s constant for this equation
The plank equation for the determination of energy differences between energy levels leads to the derivation of Rydberg’s formula. This formula relates to the different energy transitions. The Rydberg formula is given below:
𝜈 ¯=1/λ=R(1/n12−1/n22)
The electronic distribution of various electrons in orbits or shells
This phenomenon is calculated by the formula 2n2. Here, it generally shows the number of orbits in an atom.
The maximum number of electrons in the K shell is calculated by 2n2=2 x 12 = 2.
Similarly, the maximum number of electrons in the L shell is calculated by 2n2=2 x 22 = 8
The maximum number of electrons in the M shell is calculated by 2n2=2 x 32 = 18
The maximum number of electrons in the N shell is calculated by 2n2=2 x 42 = 32
The Bohrs Atomic Model for Hydrogen
A hydrogen atom (Z = 1) or a hydrogen-like ion (Z > 1), can be taken as an example to explain this model. A negatively charged electron revolves around a small positively charged nucleus in the first orbit. The absorption or emission of energy occurs during the movement of electrons from one orbit to another. The hydrogen atom produces Balmer series red light containing 656 nm wavelength when the electron moves third energy level to the second energy level.
The Bohrs atomic model for Heavier Atoms
There are more protons in the nucleus for heavier nuclei than the hydrogen atom. Bohr proposed that each electronic orbit holds only a definite number of electrons. The electron fills the lower energy level and then fills the higher energy level after filling up the lower energy level.
Limitations of Bohrs Atomic Model
There exist some limitations of Bohr’s Atomic Model which discussion is given below:
This model is unable to explain and observation of the Heisenberg Uncertainty Principle.
This model explains the calculation of function and momentum simultaneously which is a completely unthinkable issue by using the Heisenberg principle.
This model can not explain the accurate prediction of large-sized atoms and furnishes enough statistics.
This model is unable to explain the Zeeman impact issue during the splitting of the spectrum into a few wavelengths within the sight of a magnetic field.
Bohr’s Atomic Model failed to explain the matter of the Stark effect when the spectral line from the atom during excitation gets split up into fine lines in the presence of a strong electric field.
It is unable to explain the shape of the molecule.
Frequently Asked Questions (FAQ’s)
What is the definition of the Bohr atomic Model?
Bohr’s Atomic Model relates to explaining the structure & properties of negatively charged electrons revolving around the nucleus in a definite energy shell.
What are the postulates of the Bohrs Atomic Model?
This model gives the idea about orbits as well as the revolving property of negatively charged electrons. It expresses the new idea about the energy differences between the level of orbits during the movement of electrons from one orbit to another.
What are the limitations of Bohrs Atomic Model?
Bohrs atomic model cannot explain the Heisenberg Uncertainty Principle, Zeeman impact, and Stark effect in atoms. The spectral characteristic of heavy atoms can not be explained by applying the postulates of this model. The complete shape of the molecule can not be identified by this model.
How many electrons are present in K, L, M, and N shells?
K shell contains up to 2 electrons, L shell contains up to 8 electrons, M shell contains up to 18 electrons and N shell contains up to 32 electrons.